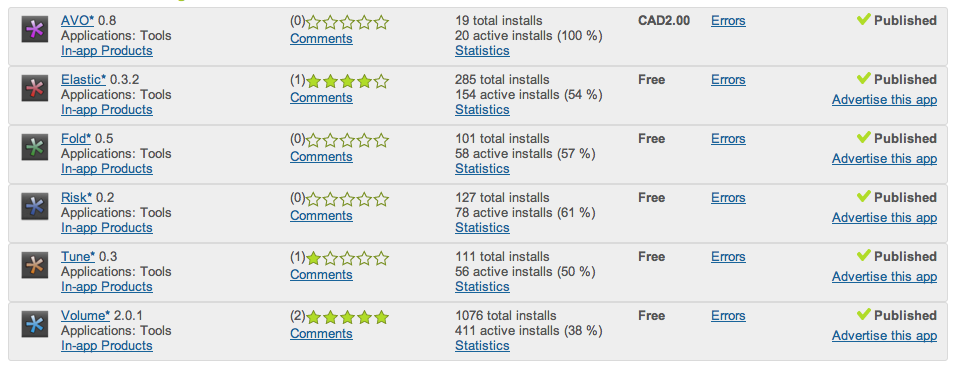
x lines of Python: AVO plot
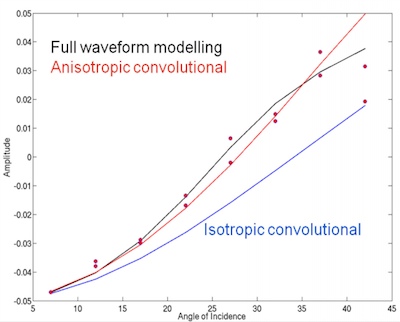
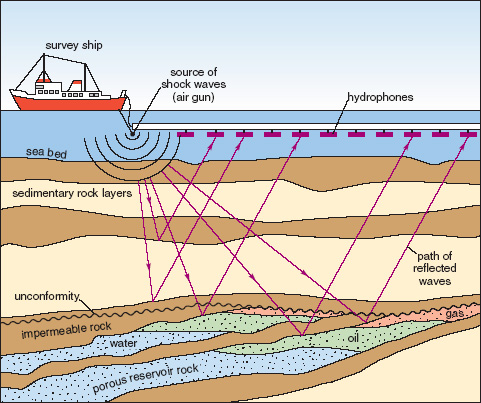
/Amplitude vs offset (or, more properly, angle) analysis is a core component of quantitative interpretation. The AVO method is based on the fact that the reflectivity of a geological interface does not depend only on the acoustic rock properties (velocity and density) on both sides of the interface, but also on the angle of the incident ray. Happily, this angular reflectivity encodes elastic rock property information. Long story short: AVO is awesome.
As you may know, I'm a big fan of forward modeling — predicting the seismic response of an earth model. So let's model the response the interface between a very simple model of only two rock layers. And we'll do it in only a few lines of Python. The workflow is straightforward:
- Define the properties of a model shale; this will be the upper layer.
- Define a model sandstone with brine in its pores; this will be the lower layer.
- Define a gas-saturated sand for comparison with the wet sand.
- Define a range of angles to calculate the response at.
- Calculate the brine sand's response at the interface, given the rock properties and the angle range.
- For comparison, calculate the gas sand's response with the same parameters.
- Plot the brine case.
- Plot the gas case.
- Add a legend to the plot.
That's it — nine lines! Here's the result:
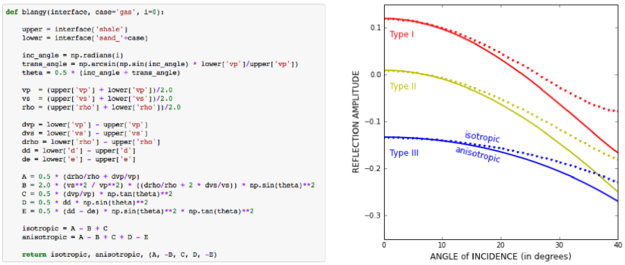
Once we have rock properties, the key bit is in the middle:
θ = range(0, 31) shuey = bruges.reflection.shuey2(vp0, vs0, ρ0, vp1, vs1, ρ1, θ)
shuey2 is one of the many functions in bruges — here it provides the two-term Shuey approximation, but it contains lots of other useful equations. Virtually everything else in our AVO plotting routine is just accounting and plotting.
As in all these posts, you can follow along with the code in the Jupyter Notebook. You can view this on GitHub, or run it yourself in the increasingly flaky MyBinder (which is down at the time of writing... I'm working on an alternative).
What would you like to see in x lines of Python? Requests welcome!












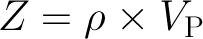








 Except where noted, this content is licensed
Except where noted, this content is licensed