Transformation in 2021
/Virtual confererences have become — for now — the norm. In many ways they are far better than traditional conferences: accessible to all, inexpensive to organize and attend, asynchronous, recorded, and no-one has to fly 5,000 km to deliver a PowerPoint. In other ways, they fall short, for example as a way to meet new collaborators or socialize with old ones. As face-to-face meetings become a possibility again this summer, smart organizations will figure out ways to get the best of both worlds.
The Software Underground is continuing its exploration of virtual events next month with the latest edition of the TRANSFORM festival of the digital subsurface. In broad strokes, here’s what’s on offer:
The Subsurface Hackathon, starting on 16 April — all are welcome, including those new to programming.
20 free & awesome tutorials, covering topics from Python to R, geothermal wells to seismic, and even reservoir simulation! And of course there’s a bit of machine learning and physics-based modeling in there too. Look forward to content from scientists in North & South America, Norway, Nigeria, and New Zealand.
Lightning talks from 24 members of the community — would you like to do one?
Birds of a Feather community meet-ups, a special Xeek challenge, and other special events.
The Annual General Meeting of the Software Underground, where we’ll adopt our by-law and appoint the board.
We’ll even try to get at that tricky “hang out with other scientists” component, because we will have a virtual Gather.town world in which to hang out and hack, chat, or watch the livestreams.
If last year’s event is anything to go by, we can expect fantastic tutorial content, innovative hackathon projects, and great conversation between at least 750 digital geoscientists and engineers. (If you missed TRANSFORM 2020, don’t worry — all the content from last year is online and free forever, so it’s not too late to take part! Check it out.)
Registering for TRANSFORM
Registration is free, or pay-what-you-like. In other words, if you have funding or expenses for conferences and training, there’s an option to pay a small amount. But anyone can attend TRANSFORM free of charge. Thank you to the event sponsors, Studio X, for making this possible. (I will write about Studio X at a later date — they are doing some really cool things in the digital subsurface.)
To register for any part of TRANSFORM — even if you just want to come to the hackathon or a tutorial — click this button and complete the process on the Software Underground website. It’s a ‘pay what you like’ event, so there are 3 registration options with different prices — these are just different donation amounts. They don’t change anything about your registration.
I hope we see you at TRANSFORM. In the meantime, please jump into the Software Underground Slack and get involved in the conversations there. (You can also catch up on recent Software Underground highlights in the new series of blog posts.)



















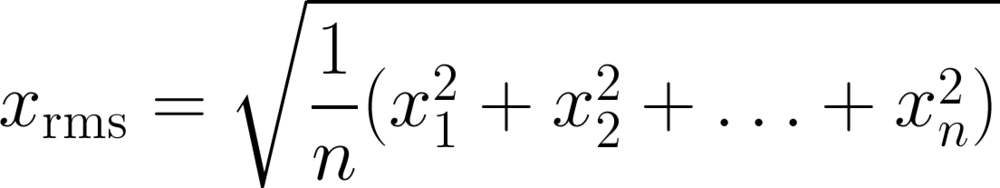

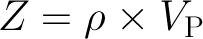








 Except where noted, this content is licensed
Except where noted, this content is licensed