Big imaging, little imaging, and telescopes
/ I caught three lovely talks at the special session yesterday afternoon, Recent Advances and the Road Ahead. Here are my notes...
I caught three lovely talks at the special session yesterday afternoon, Recent Advances and the Road Ahead. Here are my notes...
The neglected workhorse
If you were to count up all the presentations at this convention on seismic migration, only 6% of them are on time migration. Even though it is the workhorse of seismic data processing, it is the most neglected topic in migration. It's old technology, it's a commodity. Who needs to do research on time migration anymore? Sergey does.
Speaking as an academic, Fomel said, "we are used to the idea that most of our ideas are ignored by industry," even though many transformative ideas in the industry can be traced back to academics. He noted that it takes at least 5 years to get traction, and the 5 years are up for his time migration ideas, "and I'm starting to lose hope". Here's five things you probably didn't know about time migration:
- Time migration does not need travel times.
- Time migration does not need velocity analysis.
- Single offsets can be used to determine velocities.
- Time migration does need approximations, but the approximation can be made increasingly accurate.
- Time migration distorts images, but the distortion can be removed with regularized inversion.
It was joy to listen to Sergey describe these observations through what he called beautiful equations: "the beautiful part about this equation is that it has no parameters", or "the beauty of this equation is that is does not contain velocity", an so on. Mad respect.
Seismic adaptive optics
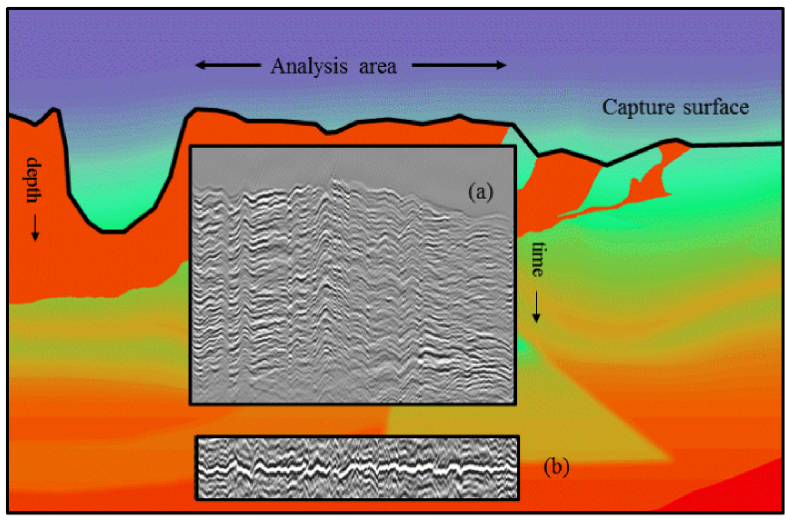 Alongside seismic multiples, poor illumination, and bandwidth limitations, John Etgen (BP) submitted that, in complex overburden, velocity is the number one problem for seismic imaging. Correct velocity model equals acceptable image. His (perhaps controversial) point was that when velocities are complex, multiples, no matter how severe, are second order thorns in the side of the seismic imager. "It's the thing that's killing us, and that's the frontier." He also posited that full waveform inversion may not save us after all, and image gather analysis looks even less promising.
Alongside seismic multiples, poor illumination, and bandwidth limitations, John Etgen (BP) submitted that, in complex overburden, velocity is the number one problem for seismic imaging. Correct velocity model equals acceptable image. His (perhaps controversial) point was that when velocities are complex, multiples, no matter how severe, are second order thorns in the side of the seismic imager. "It's the thing that's killing us, and that's the frontier." He also posited that full waveform inversion may not save us after all, and image gather analysis looks even less promising.
While FWI looks to catch the wavefield and look at it in the space of the data, migration looks to catch the wavefield and look at it at the image point itself. He elegantly explained these two paradigms, and suggested that both may be flawed.
John urged, "We need things other than what we are working on", and shared his insights from another field. In ground-based optical astronomy, for example, when the image of a star is be distorted by turbulence in our atmosphere, astromoners numerically warp the curvature of the lens to correct for rapid variations in phase of the incoming wavefront. The lenses we use for seismic focusing, velocities, can be tweaked just the same by looking at the wavefield part of the way through its propagation. He quoted Jon Claerbout:
If you want to understand how a horse runs, you gotta run along with it.
 Big imaging, little imaging, and combination of the two
Big imaging, little imaging, and combination of the two
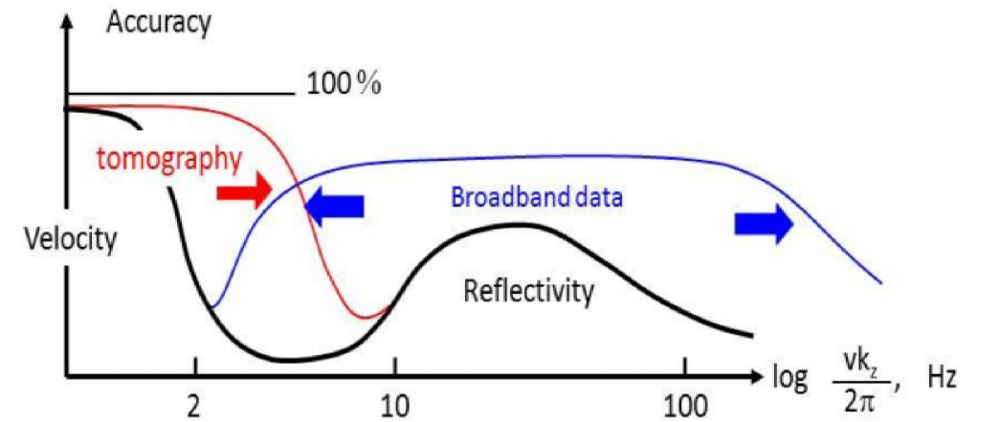
There's a number of ways one could summarize what petroleum seismologists do. But hearing (CGG researcher) Sam Gray's talk yesterday was a bit of an awakening. His talk was a remark on the notion of big imaging vs little imaging, and the need for convergence.
Big imaging is the structural stuff. Structural migration, stratigraphic imaging, wide-azimuth acquisition, and so on. It includes the hardware and compute innovations of broadband, blended sources, deblending processing, anisotropic imaging, and the beginnings of viscoacoustic reverse-time migration.
Little imaging is inversion. It's reservoir characterization. It's AVO and beyond. Azimuthal velocities (fast and slow directions) hint at fracture orientations, azimuthal amplitudes hint even more subtly at fracture compliance.
Big imaging is hard because it's computationally expensive, and velocities are unknown. Little imaging is hard because features like fractures, faults and pores are at the centimetre scale, but on land we lay out inlines and crossline hundreds of metres apart, and use signals that carry only a few bits of information from an area the size of a football field.
What we've been doing with imaging is what he called a separated workflow. We use gathers to make big images. We use gathers to make rock properties, but seldom do they meet. How often have you tested to see if the rock properties the little are explain the wiggles in the big? Our work needs to be such a cycle, if we want our relevance and impact to improve.
The figures are copyright of the authors of SEG, and used in accordance with SEG's permission guidelines.


















 Except where noted, this content is licensed
Except where noted, this content is licensed