How to cheat

Yesterday I posted the rock physics cheatsheet, which is a condensed version of useful seismic reservoir characterization and rock mechanics concepts. It's cheat as in simplify, not cheat as in swindle. 

As Matt discussed on Friday, heuristics can be shortcuts to hone your intuition. Our minds search to use rules of thumb to visualise the invisible and to solve sticky problems. That's where the cheat sheet comes in. You might not find rock physics that intuitive, but let's take a look at the table to see how it reveals some deeper patterns.

The table of elastic parameters is setup based on the fundamental notion that, if you have any two elastic properties previously defined, you can compute all the others. This is a consequence of one of the oldest laws in classical mechanics: Newton's second law, F=ma. In particular one thing I find profound about seismic velocity is that it is wholly determined by a ratio of competing tensional (elastic) forces to inertial (density) forces. To me, it is not immediately obvious that speed, with units of m/s, results from the ratio of pressure to density. 

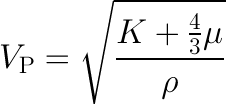
This simple little equation has had a profound impact on the utility of seismology to the oil and gas industry. It links extrinsic dynamic properties (V_P) to intrinsic rock properties (K, μ, ρ). The goal of course, is not just to investigate elastic properties for the sake of it, but to link elastic properties to reservoir and petrophysical properties. This is traditionally done using a rock physics template. The one I find easiest to understand is the V_P/V_S vs P-impedance template, an example of which is shown on the cheatsheet. You will see others in use, for instance Bill Goodway has pioneered the λρ vs μρ (LMR) template.

In an upcoming post we'll look to deepen the connection between Newtonian mechanics and reservoir characterization.